Exercise 13.1 : Solutions of Questions on Page Number : 301
Q1 :Evaluate the Given limit: 
Answer :
NCERT Solutions for Class 11 Maths Chapter 13 – Limits and Derivatives
Q2 :Evaluate the Given limit:
Answer :
Q3 :Evaluate the Given limit:
Answer :
Q4 :Evaluate the Given limit:
Answer :
Q5 :Evaluate the Given limit:
Answer :
Q6 :Evaluate the Given limit:
Answer :
Put x + 1 = y so that y → 1 as x → 0.
Q7 :Evaluate the Given limit: 
Answer :
At x = 2, the value of the given rational function takes the form 
.
Q8 :Evaluate the Given limit:
Answer :
At x = 2, the value of the given rational function takes the form 
.
Q9 :Evaluate the Given limit:
Answer :
Q10 :Evaluate the Given limit:
Answer :
At z = 1, the value of the given function takes the form
Put 
so that z →1 as x → 1.
Q11 :Evaluate the Given limit:
Answer :
Q12 :Evaluate the Given limit
Answer :
At x = -2, the value of the given function takes the form
.
Q13 :Evaluate the Given limit:
Answer :
At x = 0, the value of the given function takes the form
Q14 :Evaluate the Given limit:
Answer :
At x = 0, the value of the given function takes the form
Q15 :Evaluate the Given limit:
Answer :
It is seen that x → π ⇒ (π – x) → 0
Q16 :Evaluate the given limit:
Answer :
Q17 :Evaluate the Given limit:
Answer :
At x = 0, the value of the given function takes the form
Now,
Q18 :Evaluate the Given limit:
Answer :
At x = 0, the value of the given function takes the form
Now,
Q19 :Evaluate the Given limit:
Answer :
Q20 :Evaluate the Given limit:
Answer :
At x = 0, the value of the given function takes the form
Now,
Q21 :Evaluate the Given limit:
Answer :
At x = 0, the value of the given function takes the form ∞ – ∞
Now,
Q22 :
Answer :
At 
, the value of the given function takes the form
Now, put so that
Q23 :Find 
f(x) and
f(x), where f(x) = 
Answer :
The given function is
f(x) = 
Q24 :Find 
f(x), where f(x) =
Answer :
The given function is
Q25 :Evaluate 
f(x), where f(x) =
Answer :
The given function is
f(x) =
Q26 :Find f(x), where f(x) =
Answer :
The given function is|
Q27 :Find 
f(x), where f(x) =
Answer :
The given function is f(x) =
Q28 :Suppose f(x) = 
and if 
f(x) = f(1) what are possible values of a and b?
Answer :
The given function is
Thus, the respective possible values of a and b are 0 and 4.
Q29 :Let a1 , a2,……..,an be fixed real numbers and define a function
What is 
f(x)? For some a ≠ a1 , a2,……..,an compute 
f(x).
Answer :
The given function is
Q30 :If f(x) =
For what value (s) of a does f(x) exists?
Answer :
The given function is
When a < 0
When a > 0
Thus, exists for all a ≠ 0.
Q31 :If the function f(x) satisfies 
, evaluate 
Answer :
Q32 :If 
For what integers m and n does 
and 
exist?
Answer :
The given function is
Thus, exists if m = n.
Thus, exists for any integral value of m and n.
Exercise 13.2 : Solutions of Questions on Page Number : 312
Q1 :Find the derivative of x2 – 2 at x = 10.
Answer :
Let f(x) = x2 – 2. Accordingly,
Thus, the derivative of x2– 2 at x = 10 is 20.
Q2 :Find the derivative of 99x at x = 100.
Answer :
Let f(x) = 99x. Accordingly,
Thus, the derivative of 99x at x = 100 is 99.
Q3 :Find the derivative of x at x = 1.
Answer :
Letf(x) = x. Accordingly,
Thus, the derivative of x at x = 1 is 1.
Q4 :Find the derivative of the following functions from first principle.
(i) x3 – 27 (ii) (x – 1) (x – 2)
(ii) 
(iv)
Answer :
(i) Let f(x) = x3 – 27. Accordingly, from the first principle,
(ii) Let f(x) = (x – 1) (x – 2). Accordingly, from the first principle,
(iii) Let f(x) = Accordingly, from the first principle,
(iv) Let f(x) = Accordingly, from the first principle,
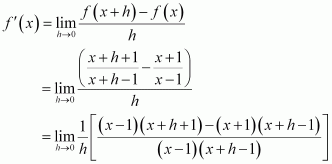
Q5 :For the function 
Prove that 
Answer :
The given function is
Thus,
Q6 :Find the derivative of 
for some fixed real number a.
Answer :
Let
Q7 :For some constants a and b, find the derivative of
(i) (x – a) (x – b) (ii) (ax2 + b)2 (iii)
Answer :
(i) Let f (x) = (x – a) (x – b)
(ii) Let f(x) = (ax2 + b)2
(iii) let f(x) =
By quotient rule,
Q8 :Find the derivative of 
for some constant a.
Answer :
By quotient rule,
Q9 :Find the derivative of
(i)
(ii) (5x3 + 3x – 1) (x – 1)
(iii) x-3 (5 + 3x) (iv) x5 (3 – 6x-9)
(v) x-4 (3 – 4x-5) (vi)
Answer :
(i) Let f(x) =
(ii) Let f (x) = (5x3 + 3x – 1) (x – 1)
By Leibnitz product rule,
(iii) Let f (x) = x– 3 (5 + 3x)
By Leibnitz product rule,
(iv) Let f (x) = x5 (3 – 6x-9)
By Leibnitz product rule,
(v) Let f (x) = x-4 (3 – 4x-5)
By Leibnitz product rule,
(vi) Let f (x) = 
By quotient rule,
Q10 :Find the derivative of cos x from first principle.
Answer :
Let f (x) = cos x. Accordingly, from the first principle,
Q11 :Find the derivative of the following functions:
(i) sin x cos x (ii) sec x (iii) 5 sec x + 4 cos x
(iv) cosec x (v) 3cot x + 5cosec x
(vi) 5sin x – 6cos x + 7 (vii) 2tan x – 7sec x
Answer :
(i) Let
f (x) = sin x cos x. Accordingly, from the first principle,
(ii) Let f (x) = sec x. Accordingly, from the first principle,
(iii) Letf (x) = 5 sec x + 4 cos x. Accordingly, from the first principle,
(iv) Let f (x) = cosec x. Accordingly, from the first principle,
(v) Let f (x) = 3cot x + 5cosec x. Accordingly, from the first principle,
From (1), (2), and (3), we obtain
(vi) Let f (x) = 5sin x – 6cos x + 7. Accordingly, from the first principle,
(vii) Let f (x) = 2 tan x -7 sec x. Accordingly, from the first principle,
Exercise Miscellaneous : Solutions of Questions on Page Number : 317
Q1 :Find the derivative of the following functions from first principle:
(i) -x (ii) (-x)-1 (iii) sin (x + 1)
(iv)
Answer :
(i) Let f(x) = -x. Accordingly f (x+h)= -(x+h)
By first principle,
(ii) Let 
Accordingly,
By first principle,
(iii) Let f(x) = sin (x + 1). Accordingly, f (x+h) =sin (x+h+1)
By first principle,
(iv) Let
Accordingly, 
By first principle,
Q2 :Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): (x + a)
Answer :
Let f(x) = x + a. Accordingly, f(x+h) = x + h + a
By first principle,
Q3 :Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): 
Answer :
By Leibnitz product rule,
Q4 :Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): (ax + b) (cx + d)2
Answer :
Let f (x) = (ax + b) (cx + d)2
By Leibnitz product rule,
Q5 :Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers):
Answer :
Let f(x) =
By quotient rule,
Q6 :Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): 
Answer :
By quotient rule,
Q7 :Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers):
Answer :
Let 
By quotient rule,
Q8 :Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers):
Answer :
By quotient rule,
Q9 :Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers):
Answer :
By quotient rule,
Q10 :Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers):
Answer :
Q11 :Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers):
Answer :
Q12 :Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): (ax + b)n
Answer :
By first principle,
Q13 :Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): (ax + b)n (cx + d)m
Answer :
Let f(x) =(ax + b)n (cx + d)m
By Leibnitz product rule,
Therefore, from (1), (2), and (3), we obtain
Q14 :Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): sin (x + a)
Answer :
Let f(x) = sin(x+a)
f (h+x) =sin ( h + x+ a)
By first principle,
Q15 :Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): cosec x cot x
Answer :
Let f(x) = cosec x cot x
By Leibnitz product rule,
By first principle,
Now, let f2(x) = cosec x. Accordingly,
By first principle,
From (1), (2), and (3), we obtain
Q16 :Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers):
Answer :
Let 
By quotient rule,
Q17 :Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers):
Answer :
Let 
By quotient rule,
Q18 :Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers):
Answer :
Let
By quotient rule,
Q19 :Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): sinn x
Answer :
Let y = sinn x.
Accordingly, for n = 1, y = sin x.
For n = 2, y = sin2 x.
For n = 3, y = sin3 x.
We assert that
Let our assertion be true for n = k.
i.e.,
Thus, our assertion is true for n = k + 1.
Hence, by mathematical induction,
Q20 :Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers):
Answer :
By quotient rule,
Q21 :Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers):
Answer :
Let
By quotient rule,
By first principle,
From (i) and (ii), we obtain
Q22 :Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): x4 (5 sin x – 3 cos x)
Answer :
Let f(x) =x4 (5 sin x – 3 cos x)
By product rule,
Q23 :Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): (x2 + 1) cos x
Answer :
Let f(x) = (x2 + 1) cos x
By product rule,
Q24 :Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): (ax2 + sin x) (p + q cos x)
Answer :
Let f(x) = (ax2 + sin x) (p + q cos x)
By product rule,
Q25 :Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): (x + cosx) (x -tanx)
Answer :
Let f(x) = (x + cosx) (x -tanx)
By product rule,
Let. Accordingly,
By first principle,
Therefore, from (i) and (ii), we obtain
Q26 :Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers):
Answer :
Let 
By quotient rule,
Q27 :Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers):
Answer :
Let 
By quotient rule,
Q28 :Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers):
Answer :
Let 
By first principle,
From (i) and (ii), we obtain
Q29 :Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): (x + sec x) (x – tan x)
Answer :
Let f(x)= (x + sec x) (x – tan x)
By product rule,
From (i), (ii), and (iii), we obtain
Q30 :Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers):
Answer :
Let 
By quotient rule,
It can be easily shown that 
Therefore,
