NCERT Solutions for Class 11 Maths Chapter 8 Binomial Theorem is an essential study material for students who are preparing for their senior secondary examinations. The chapter covers the fundamental principles and concepts of the binomial theorem and its applications in various fields of mathematics. The solutions provided in this chapter are structured in a simple and concise manner, making it easy for students to understand the concepts and score good marks in their exams.
Exercise 8.1 : Solutions of Questions on Page Number : 166
NCERT Solution Class 11 Maths Chapter 8 Binomial theorem
Q1 : Expand the expression (1- 2x)5
Answer :
By using Binomial Theorem, the expression (1- 2x)5 can be expanded as
Q2 : Expand the expression 
Answer :
By using Binomial Theorem, the expression can be expanded as
Q3 : Expand the expression (2x – 3)6
Answer :
By using Binomial Theorem, the expression (2x- 3)6 can be expanded as
Q4 : Expand the expression 
Answer :
By using Binomial Theorem, the expression can be expanded
Q5 : Expand 
Answer :
By using Binomial Theorem, the expression can be expanded as
Q6 : Using Binomial Theorem, evaluate (96)3
Answer :
96 can be expressed as the sum or difference of two numbers whose powers are easier to calculate and then, binomial theorem can be applied.
It can be written that, 96 = 100 – 4
Q7 : Using Binomial Theorem, evaluate (102)5
Answer :
102can be expressed as the sum or difference of two numbers whose powers are easier to calculate and then, Binomial Theorem can be applied.
It can be written that, 102 = 100 + 2
Q8 : Using Binomial Theorem, evaluate (101)4
Answer :
101 can be expressed as the sum or difference of two numbers whose powers are easier to calculate and then, Binomial Theorem can be applied.
It can be written that, 101 = 100 + 1
Q9 : Using Binomial Theorem, evaluate (99)5
Answer :
99 can be written as the sum or difference of two numbers whose powers are easier to calculate and then, Binomial Theorem can be applied.
It can be written that, 99 = 100 – 1
Q10 : Using Binomial Theorem, indicate which number is larger (1.1)10000 or 1000.
Answer :
By splitting 1.1 and then applying Binomial Theorem, the first few terms of (1.1)10000can be obtained as
Q11 : Find (a + b)4– (a- b)4. Hence, evaluate 
Answer :
Using Binomial Theorem, the expressions, (a+ b)4and (a – b)4, can be expanded a
Q12 : Find (x+ 1)6+ (x -1)6. Hence or otherwise evaluate 
.
Answer :
Using Binomial Theorem, the expressions, (x+ 1)6 and (x – 1)6, can be expanded as
By putting, we obtain
Q13 : Show that 
is divisible by 64, whenever nis a positive integer.
Answer :
In order to show that is divisible by 64, it has to be proved that,
, where k is some natural number
By Binomial Theorem,
For a = 8 and m = n+ 1, we obtain
Thus, is divisible by 64, whenever n is a positive integer.
Q14 : Prove that 
Answer :
By Binomial Theorem,
By putting b= 3 and a= 1 in the above equation, we obtain
Hence, proved.
Exercise 8.2 : Solutions of Questions on Page Number : 171
Q1 : Find the coefficient of x5in (x + 3)8
Answer :
It is known that (r + 1)th term, (Tr+1), in the binomial expansion of (a + b)n is given by 
.
Assuming that x5 occurs in the (r+ 1)th term of the expansion (x+ 3)8, we obtain
Comparing the indices of x in x5 and in Tr+1, we obtain
r= 3
Thus, the coefficient of x5 is 
Q2 : Find the coefficient of a5b7in (a – 2b)12
Answer :
It is known that (r + 1)th term, (Tr+1), in the binomial expansion of (a + b)n is given by
Assuming that a5b7 occurs in the (r+ 1)thterm of the expansion (a- 2b)12, we obtain
Comparing the indices of aand b in a5b7 and in Tr+1, we obtain
r= 7
Thus, the coefficient of a5b7 is 
Q3 : Write the general term in the expansion of (x2– y)6
Answer :
It is known that the general term Tr+1 {which is the (r + 1)th term} in the binomial expansion of (a + b)n is given by .
Thus, the general term in the expansion of (x2– y6) is
Q4 : Write the general term in the expansion of (x2– yx)12, x ≠0
Answer :
It is known that the general term Tr+1 {which is the (r + 1)th term} in the binomial expansion of (a + b)n is given
by
Thus, the general term in the expansion of(x2-yx)12 is 
Q5 : Find the 4th term in the expansion of (x- 2y)12 .
Answer :
It is known that (r + 1)th term, (Tr+1), in the binomial expansion of (a + b)n is given by .
Thus, the 4thterm in the expansion of (x- 2y)12 is 
Q6 : Find the 13th term in the expansion of 
.
Answer :
It is known that (r + 1)th term, (Tr+1), in the binomial expansion of (a + b)n is given by .
Thus, 13th term in the expansion of is
Q7 : Find the middle terms in the expansions of 
Answer :
It is known that in the expansion of (a+ b)n, if n is odd, then there are two middle terms, namely,
term and 
term.
Therefore, the middle terms in the expansion of are 
term and 
term
Thus, the middle terms in the expansion of are 
.
Q8 : Find the middle terms in the expansions of 
Answer :
It is known that in the expansion (a+ b)n, if n is even, then the middle term is term.
Therefore, the middle term in the expansion of 
is 
term
Thus, the middle term in the expansion of is 61236 x5y5.
Q9 : In the expansion of (1 + a)m + n, prove that coefficients of am and an are equal.
Answer :
It is known that (r + 1)th term, (Tr+1), in the binomial expansion of (a + b)n is given by .
Assuming that amoccurs in the (r+ 1)th term of the expansion (1 + a)m+ n, we obtain
Comparing the indices of ain amand in Tr + 1, we obtain
r= m
Therefore, the coefficient of am is
Assuming that anoccurs in the (k+ 1)th term of the expansion (1 + a)m+n, we obtain
Comparing the indices of ain anand in Tk+ 1, we obtain
k= n
Therefore, the coefficient of an is
Thus, from (1) and (2), it can be observed that the coefficients of am and an in the expansion of (1 + a)m+ n are equal.
Q10 : The coefficients of the (r- 1)th, rth and (r + 1)th terms in the expansion of
(x+ 1)n are in the ratio 1:3:5. Find nand r.
Answer :
It is known that (k + 1)th term, (Tk+1), in the binomial expansion of (a + b)n is given by 
Therefore, (r – 1)th term in the expansion of (x+ 1)n is 
rth term in the expansion of (x+ 1)n is 
(r+ 1)th term in the expansion of (x+ 1)n is 
Therefore, the coefficients of the (r- 1)th, rth, and (r + 1)th terms in the expansion of (x+ 1)n are 
respectively.
Since these coefficients are in the ratio 1:3:5, we obtain
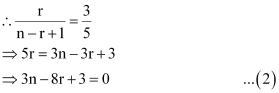
Multiplying (1) by 3 and subtracting it from (2), we obtain
4r – 12 = 0
⇒ r= 3
Putting the value of rin (1), we obtain
n- 12 + 5 = 0
⇒ n= 7
Thus, n = 7 and r = 3
Q11 : Prove that the coefficient of xn in the expansion of (1 + x)2n is twice the coefficient of xn in the expansion of (1 + x)2n-1 .
Answer :
It is known that (r + 1)th term, (Tr+1), in the binomial expansion of (a + b)n is given by .
Assuming that xn occurs in the (r+ 1)th term of the expansion of (1 + x)2n, we obtain
Comparing the indices of x in xn and in Tr+ 1, we obtain
r= n
Therefore, the coefficient of xn in the expansion of (1 + x)2n is
Assuming that xn occurs in the (k+1)th term of the expansion (1 + x)2n – 1, we obtain
Comparing the indices of x in xn and Tk+ 1, we obtain
k= n
Therefore, the coefficient of xn in the expansion of (1 + x)2n -1 is
From (1) and (2), it is observed that
Therefore, the coefficient of xn in the expansion of (1 + x)2n is twice the coefficient of xn in the expansion of (1 + x)2n-1.
Hence, proved.
Q12 : Find a positive value of m for which the coefficient of x2 in the expansion
(1 + x)m is 6.
Answer :
It is known that (r + 1)th term, (Tr+1), in the binomial expansion of (a + b)n is given by .
Assuming that x2 occurs in the (r + 1)th term of the expansion (1 +x)m, we obtain
Comparing the indices of x in x2 and in Tr+ 1, we obtain
r= 2
Therefore, the coefficient of x2 is 
.
It is given that the coefficient of x2 in the expansion (1 + x)m is 6.
Thus, the positive value of m, for which the coefficient of x2 in the expansion
(1 + x)m is 6, is 4.
Exercise Miscellaneous : Solutions of Questions on Page Number : 175
Q1 : Find a, band n in the expansion of (a+ b)n if the first three terms of the expansion are 729, 7290 and 30375,
respectively.
Answer :
It is known that (r + 1)th term, (Tr+1), in the binomial expansion of (a + b)n is given by .
The first three terms of the expansion are given as 729, 7290, and 30375 respectively.
Therefore, we obtain
Dividing (2) by (1), we obtain
Dividing (3) by (2), we obtain
From (4) and (5), we obtain
Substituting n = 6 in equation (1), we obtain
a6= 729
From (5), we obtain
Thus, a = 3, b= 5, and n= 6.
Q2 : Find a if the coefficients of x2 and x3 in the expansion of (3 + ax)9 are equal.
Answer :
It is known that (r + 1)th term, (Tr+1), in the binomial expansion of (a + b)n is given by .
Assuming that x2occurs in the (r+ 1)thterm in the expansion of (3 + ax)9, we obtain
Comparing the indices of x in x2 and in Tr+ 1, we obtain
r= 2
Thus, the coefficient of x2 is
Assuming that x3 occurs in the (k+ 1)th term in the expansion of (3 + ax)9, we obtain
Comparing the indices of x in x3 and in Tk+ 1, we obtain
k = 3
Thus, the coefficient of x3 is
It is given that the coefficients of x2 and x3 are the same.
Thus, the required value of a is.
Q3 : Find the coefficient of x5in the product (1 + 2x)6(1 – x)7 using binomial theorem.
Answer :
Using Binomial Theorem, the expressions, (1 + 2x)6 and (1 – x)7, can be expanded as
The complete multiplication of the two brackets is not required to be carried out. Only those terms, which involve x5, are required.
The terms containing x5 are
Thus, the coefficient of x5 in the given product is 171.
Q4 : If a and b are distinct integers, prove that a – b is a factor of an – bn, whenever n is a positive integer.
[Hint: write an = (a – b + b)n and expand]
Answer :
In order to prove that (a- b) is a factor of (an– bn), it has to be proved that
an– bn= k (a- b), where k is some natural number
It can be written that, a= a – b + b
This shows that (a- b) is a factor of (an– bn), where n is a positive integer.
Q5 : Evaluate 
.
Answer :
Firstly, the expression (a+ b)6– (a- b)6 is simplified by using Binomial Theorem.
This can be done as
Q6 : Find the value of 
.
Answer :
Firstly, the expression (x+ y)4+ (x – y)4 is simplified by using Binomial Theorem.
This can be done as
Q7 : Find an approximation of (0.99)5 using the first three terms of its expansion.
Answer :
0.99 = 1 – 0.01
Thus, the value of (0.99)5 is approximately 0.951.
Q8 : Find n, if the ratio of the fifth term from the beginning to the fifth term from the end in the expansion of 
Answer :
In the expansion, 
,
Fifth term from the beginning 
Fifth term from the end 
Therefore, it is evident that in the expansion of 
, the fifth term from the beginning is 
and the fifth term from the end is 
.
It is given that the ratio of the fifth term from the beginning to the fifth term from the end is 
. Therefore, from (1) and (2), we obtain
Thus, the value of n is 10.
Q9 : Expand using Binomial Theorem 
.
Answer :
Using Binomial Theorem, the given expression 
can be expanded as
Again by using Binomial Theorem, we obtain
From(1), (2), and (3), we obtain
Q10 : Find the expansion of 
using binomial theorem.
Answer :
Using Binomial Theorem , the given expression can be expanded as
Again by using Binomial Theorem, we obtain
From (1) and (2), we obtain
