NCERT Solutions for Class 12 Maths Part 2 Chapter 7 Integrals

Free NCERT Solutions for Class 12 Maths Chapter 7 Integrals solved by Expert Teachers as per NCERT (CBSE) Book guidelines and brought to you by Toppers Bulletin. These Integrals Exercise Questions with Solutions for Class 12 Maths covers all questions of Chapter Integrals Class 12 and help you to revise complete Syllabus and Score More marks as per CBSE Board guidelines from the latest NCERT book for class 12 maths. You can read and download NCERT Book Solution to get a better understanding of all topics and concepts
7.1 Introduction
7.2 Integration as an Inverse Process of Differentiation
7.2.1 Geometrical interpretation of indefinite integral
7.2.2 Some properties of indefinite integral
7.2.3 Comparison between differentiation and integration
7.3 Methods of Integration
7.3.1 Integration by substitution
7.3.2 Integration using trigonometric identities
7.4 Integrals of Some Particular Functions
7.5 Integration by Partial Fractions
7.6 Integration by Parts
7.6.1 Integral of the type
7.6.2 Integrals of some more types
7.7 Definite Integral
7.7.1 Definite integral as the limit of a sum
7.8 Fundamental Theorem of Calculus
7.8.1 Area function
7.8.2 First fundamental theorem of integral calculus
7.8.3 Second fundamental theorem of integral calculus
7.9 Evaluation of Definite Integrals by Substitution
7.10 Some Properties of Definite Integrals.

Integrals NCERT Solutions – Class 12 Maths

Exercise 7.1 : Solutions of Questions on Page Number : 299
Q1 :sin 2x
Answer :The anti derivative of sin 2x is a function of x whose derivative is sin 2x.
It is known that,

Therefore, the anti derivative of

Q2 :Cos 3x
Answer : The anti derivative of cos 3x is a function of x whose derivative is cos 3x.
It is known that,

Therefore, the anti derivative of .

Q3 :e2x
Answer :The anti derivative of e2x is the function of x whose derivative is e2x.
It is known that,

Therefore, the anti derivative of .

Q4 :
Answer :The anti derivative of is the function of x whose derivative is .
It is known that,

Therefore, the anti derivative of

Q5 :
Answer :
The anti derivative of is the function of x whose derivative is
It is known that,

Therefore, the anti derivative of is .

Q6 :
Answer :

Q7 :
Answer :

Q8 :
Answer :

Q9 :
Answer :

Q10 :
Answer :

Q11 :
Answer :

Q12 :
Answer :

Q13 :
Answer :

On dividing, we obtain

Q14 :
Answer :

Q15 :
Answer :

Q16 :
Answer :

Q17 :
Answer :

Q18 :
Answer :

Q19 :
Answer :

Q20 :
Answer :

Q21 :The anti derivative of equals
(A) (B)
(C) (D)
Answer :

Hence, the correct answer is C.

Q22 :If such that f(2) = 0, then f(x) is
(A) (B)
(C) (D)
Answer :It is given that,
∴Anti derivative of
∴
Also,
Hence, the correct answer is A.

Exercise 7.2 : Solutions of Questions on Page Number : 304

Q1 :
Answer :
Let = t
∴2x dx = dt

Q2 :
Answer :
Let log |x| = t
∴

Q3 :
Answer :
Let 1 + log x = t
∴

Q4 :sin x . sin (cos x)
Answer : sin x Ã¢â€¹â€¦ sin (cos x)
Let cos x = t
∴ – sin x dx = dt

Q5 :
Answer :
Let∴ 2adx = dt

Q6 :
Answer :
Let ax + b = t
⇒ adx = dt

Q7 :
Answer :Let
∴ dx = dt

Q8 :
Answer :
Let 1 + 2×2 = t
∴ 4xdx = dt

Q9 :
Answer :
Let
∴ (2x + 1)dx = dt

Q10 :
Answer :
Let

∴

Q11 :
Answer :

Q12 :
Answer :
Let

∴

Q13 :
Answer :
Let
∴ 9×2 dx = dt

Q14 :
Answer :
Let log x = t
∴

Q15 :
Answer :
Let∴ – 8x dx = dt

Q16 :
Answer :
Let∴ 2dx = dt

Q17 :
Answer :
Let∴ 2xdx = dt

Q18 :
Answer :
Let

Q19 :
Answer :
Dividing numerator and denominator by ex, we obtain

Let
∴

Q20 :
Answer :
Let
∴

Q21 :
Answer :

Let 2x – 3 = t
∴ 2dx = dt

Q22 :
Answer :
Let 7 – 4x = t
∴ – 4dx = dt

Q23 :
Answer :
Let
∴

Q24 :
Answer :
Let
∴

Q25 :
Answer :
Let
∴

Q26 :
Answer :
Let
∴

Q27 :
Answer :
Let sin 2x = t
∴

Q28 :
Answer :
Let∴ cos x dx = dt

Q29 :cot x log sin x
Answer :
Let log sin x = t

Q30 :
Answer :
Let 1 + cos x = t
∴ – sin x dx = dt

Q31 :
Answer :
Let 1 + cos x = t
∴ – sin x dx = dt

Q32 :
Answer :

Let sin x + cos x = t ⇒ (cos x – sin x) dx = dt

Q33 :
Answer :

Put cos x – sin x = t ⇒ ( – sin x – cos x) dx = dt

Q34 :
Answer :

Q35 :
Answer :
Let 1 + log x = t
∴

Q36 :
Answer :
Let
∴

Q37 :
Answer :
Let x4 = t
∴ 4x3dx = dt

Let
∴
From (1), we obtain

Q38 :equals

Answer :
Let
∴

Hence, the correct answer is D.

Q39 :equals

Answer :
Let
∴

Hence, the correct answer is D.

Exercise 7.3 : Solutions of Questions on Page Number : 307

Q1 :
Answer :

Q2 :
Answer :
It is known that,

Q3 : cos 2x cos 4x cos 6x
Answer :
It is known that,

Q4 : sin3 (2x + 1)
Answer :
Let

Q5 : sin3 x cos3 x
Answer :

Q6 : sin x sin 2x sin 3x
Answer :
It is known that,

Q7 : sin 4x sin 8x
Answer :
It is known that,

Q8 :
Answer :

Q9 :
Answer :

Q10 : sin4 x
Answer :

Q11 : cos4 2x
Answer :

Q12 :
Answer :

Q13 :
Answer :

Q14 :
Answer :

Q15 :
Answer :

Q16 : tan4x
Answer :

From equation (1), we obtain

Q17 :
Answer :

Q18 :
Answer :

Q19 :
Answer :

Q20 :
Answer :

Q21 : sin-1 (cos x)
Answer :

It is known that,

Substituting in equation (1), we obtain

Q22 :
Answer :

Q23 :is equal to
A. tan x + cot x + C
B. tan x + cosec x + C
C. – tan x + cot x + C
D. tan x + sec x + C
Answer :

Hence, the correct answer is A.

Q24 :equals
A. – cot (exx) + C
B. tan (xex) + C
C. tan (ex) + C
D. cot (ex) + C
Answer :
Let exx = t

Hence, the correct answer is B.

Exercise 7.4 : Solutions of Questions on Page Number : 315

Q1 :
Answer :
Let x³ = t
∴ 3x² dx = dt

Q2 :
Answer :
Let 2x = t
∴ 2dx = dt

Q3 :
Answer :
Let 2 – x = t
⇒ – dx = dt

Q4 :
Answer :
Let 5x = t
∴ 5dx = dt

Q5 :
Answer :

Q6 :
Answer :
Let x3 = t
∴ 3×2 dx = dt

Q7 :
Answer :

From (1), we obtain

Q8 :
Answer :
Let x³ = t
⇒ 3x² dx = dt

Q9 :
Answer :
Let tan x = t
∴ sec²x dx = dt

Q10 :
Answer :

Q12 :
Answer :

Q13 :
Answer :

Q14 :
Answer :

Q15 :
Answer :

Q16 :
Answer :

Equating the coefficients of x and constant term on both sides, we obtain
4A = 4 ⇒ A = 1
A + B = 1 ⇒ B = 0
Let 2×2 + x – 3 = t
∴ (4x + 1) dx = dt

Q17 :
Answer :

Equating the coefficients of x and constant term on both sides, we obtain

From (1), we obtain

From equation (2), we obtain

Q18 :
Answer:

Equating the coefficients of x and constant term on both sides, we obtain

Substituting equations (2) and (3) in (1), we obtain

Q19 :
Answer :Answre

Equating the coefficients of x and constant term, we obtain
2A = 6 ⇒ A = 3
– 9A + B = 7 ⇒ B = 34
∴ 6x + 7 = 3 (2x – 9) + 34

Substituting equations (2) and (3) in (1), we obtain

Q20 :
Answer :

Equating the coefficients of x and constant term on both sides, we obtain

Using equations (2) and (3) in (1), we obtain

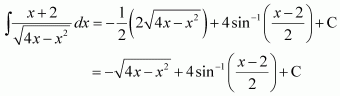
Q21 :
Answer :

Let x² + 2x +3 = t
⇒ (2x + 2) dx =dt

Using equations (2) and (3) in (1), we obtain

Q22 :
Answer :

Equating the coefficients of x and constant term on both sides, we obtain

Substituting (2) and (3) in (1), we obtain

Q23 :
Answer :

Equating the coefficients of x and constant term, we obtain

Using equations (2) and (3) in (1), we obtain

Q24 :equals
A. x tan – 1 (x + 1) + C
B. tan – 1 (x + 1) + C
C. (x + 1) tan – 1 x + C
D. tan – 1x + C
Answer :

Hence, the correct answer is B.

Q25 :equals
A.
B.
C.
D.
Answer :

Hence, the correct answer is B.

Exercise 7.5 : Solutions of Questions on Page Number : 322

Q1 :
Answer :
Let
Equating the coefficients of x and constant term, we obtain
A + B = 1
2A + B = 0
On solving, we obtain
A = – 1 and B = 2

Q2 :
Answer :
Let

Equating the coefficients of x and constant term, we obtain
A + B = 0
– 3A + 3B = 1
On solving, we obtain

Q3 :
Answer :
Let

Substituting x = 1, 2, and 3 respectively in equation (1), we obtain
A = 1, B = – 5, and C = 4

Q4 :
Answer :
Let
Substituting x = 1, 2, and 3 respectively in equation (1), we obtain

Q5 :
Answer :
Let
Substituting x = – 1 and – 2 in equation (1),we obtain
A = – 2 and B = 4

Q6 :
Answer :
It can be seen that the given integrand is not a proper fraction.
Therefore, on dividing (1 – x²) by x(1 – 2x), we obtain

Let

Substituting x = 0 and in equation (1), we obtain
A = 2 and B = 3

Substituting in equation (1), we obtain

Q7 :
Answer :
Let

Equating the coefficients of x², x, and constant term, we obtain
A + C = 0
– A + B = 1
– B + C = 0
On solving these equations, we obtain

From equation (1), we obtain

Q8 :
Answer :
Let
Substituting x = 1, we obtain

Equating the coefficients of x² and constant term, we obtain
A + C = 0
– 2A + 2B + C = 0
On solving, we obtain

Q9 :
Answer :
Let

Substituting x = 1 in equation (1), we obtain
B = 4
Equating the coefficients of x² and x, we obtain
A + C = 0
B – 2C = 3
On solving, we obtain

Q10 :
Answer :

Let

Equating the coefficients of x2 and x, we obtain

Q11 :
Answer :

Let

Substituting x = – 1, – 2, and 2 respectively in equation (1), we obtain

Q12 :
Answer :
It can be seen that the given integrand is not a proper fraction.
Therefore, on dividing (x³ + x + 1) by x² – 1, we obtain

Let

Substituting x = 1 and – 1 in equation (1), we obtain

Q13 :
Answer :

Equating the coefficient of x², x, and constant term, we obtain
A – B = 0
B – C = 0
A + C = 2
On solving these equations, we obtain
A = 1, B = 1, and C = 1

Q14 :
Answer :

Equating the coefficient of x and constant term, we obtain
A = 3
2A + B = – 1 ⇒ B = – 7

Q15 :
Answer :

Equating the coefficient of x³, x², x, and constant term, we obtain

On solving these equations, we obtain

Q16 :[Hint: multiply numerator and denominator by x^{n – 1} and put xⁿ = t]
Answer :

Multiplying numerator and denominator by x^{n – 1}, we obtain

Substituting t = 0, – 1 in equation (1), we obtain
A = 1 and B = – 1

Q17 :[Hint: Put sin x = t]
Answer :

Substituting t = 2 and then t = 1 in equation (1), we obtain
A = 1 and B = – 1

Q18 :
Answer :

Equating the coefficients of x³, x², x, and constant term, we obtain
A + C = 0
B + D = 4
4A + 3C = 0
4B + 3D = 10
On solving these equations, we obtain
A = 0, B = – 2, C = 0, and D = 6

Q19 :
Answer :

Let x² = t ⇒ 2x dx = dt

Substituting t = – 3 and t = – 1 in equation (1), we obtain

Q20 :
Answer :

Multiplying numerator and denominator by x³, we obtain

Let x4 = t ⇒ 4x3dx = dt

Substituting t = 0 and 1 in (1), we obtain
A = – 1 and B = 1

Q21 :[Hint: Put e^x = t]
Answer :

Let e^x = t ⇒ e^x dx = dt

Substituting t = 1 and t = 0 in equation (1), we obtain
A = – 1 and B = 1

Q22 :
A.
B.
C.
D.
Answer :

Substituting x = 1 and 2 in (1), we obtain
A = – 1 and B = 2

Hence, the correct answer is B.

Q23 :
A.
B.
C.
D.
Answer :

Equating the coefficients of x², x, and constant term, we obtain
A + B = 0
C = 0
A = 1
On solving these equations, we obtain
A = 1, B = – 1, and C = 0

Hence, the correct answer is A.

Exercise 7.6 : Solutions of Questions on Page Number : 327

Q1 : x sin x
Answer :
Let I =
Taking x as first function and sin x as second function and integrating by parts, we obtain

Q2 :
Answer :
Let I =
Taking x as first function and sin 3x as second function and integrating by parts, we obtain

Q3 :
Answer :
Let
Taking x² as first function and ex as second function and integrating by parts, we obtain

Again integrating by parts, we obtain

Q4 : x logx
Answer :
Let
Taking log x as first function and x as second function and integrating by parts, we obtain

Q5 :x log 2x
Answer :
LetTaking log 2x as first function and x as second function and integrating by parts, we obtain

Q6 : x² log x
Answer :
LetTaking log x as first function and x² as second function and integrating by parts, we obtain

Q7 :
Answer :
Let
Taking as first function and x as second function and integrating by parts, we obtain

Q8 :
Answer :
Let
Taking as first function and x as second function and integrating by parts, we obtain

Q9 :
Answer :
Let
Taking cos – 1 x as first function and x as second function and integrating by parts, we obtain

Q10 :
Answer :
Let
Taking as first function and 1 as second function and integrating by parts, we obtain

Q11 :
Answer :
Let

Taking as first function and as second function and integrating by parts, we obtain

Q12 :
Answer :
Let
Taking x as first function and sec2x as second function and integrating by parts, we obtain

Q13 :
Answer :
Let
Taking as first function and 1 as second function and integrating by parts, we obtain

Q14 :
Answer :
Taking as first function and x as second function and integrating by parts, we obtain

Q15 :
Answer :
Let
Let I = I₁ + I₂ … (1)
Where,and
Taking log x as first function and x² as second function and integrating by parts, we obtain

Taking log x as first function and 1 as second function and integrating by parts, we obtain

Using equations (2) and (3) in (1), we obtain

Q16 :
Answer :
Let
Let
⇒
∴
It is known that,

Q17 :
Answer :
Let

Let
⇒
It is known that,

Q18 :
Answer :

Let⇒
It is known that,
From equation (1), we obtain

Q19 :
Answer :
Also, let ⇒
It is known that,

Q20 :
Answer :

Let

⇒
It is known that,

Q21:
Answer :
Let
Integrating by parts, we obtain

Again integrating by parts, we obtain

Q22 :
Answer :
Let ⇒
= 2θ
⇒
Integrating by parts, we obtain

Q23 :equals

Answer :
Let
Also, let ⇒

Hence, the correct answer is A.

Q24 :equals

Answer :

Let
Also, let ⇒
It is known that,

Hence, the correct answer is B.

Exercise 7.7 : Solutions of Questions on Page Number : 330

Q1 :
Answer :

Q2 :
Answer :

Q3 :

Answer :

Q4 :
Answer :

Q5 :
Answer :

Q6 :
Answer :

Q7 :
Answer :

Q8 :
Answer :

Q9 :
Answer :

Q10 :is equal to
A.
B.
C.
D.
Answer :

Hence, the correct answer is A.

Q11 :is equal to
A.
B.
C.
D.
Answer :

Hence, the correct answer is D.

Exercise 7.8 : Solutions of Questions on Page Number : 334

Q1 :
Answer :
It is known that,

Q2 :
Answer :
It is known that,

Q3 :
Answer :
It is known that,

Q4 :
Answer :

It is known that,

From equations (2) and (3), we obtain

Q5 :
Answer :

It is known that,

Q6 :
Answer :
It is known that,

Exercise 7.9 : Solutions of Questions on Page Number : 338

Q1 :
Answer :

By second fundamental theorem of calculus, we obtain

Q2 :
Answer :

By second fundamental theorem of calculus, we obtain

Q3 :
Answer :

By second fundamental theorem of calculus, we obtain

Q4 :
Answer :

By second fundamental theorem of calculus, we obtain

Q5 :
Answer :

By second fundamental theorem of calculus, we obtain

Q6 :
Answer :

By second fundamental theorem of calculus, we obtain

Q7 :
Answer :

By second fundamental theorem of calculus, we obtain

Q8 :
Answer :

By second fundamental theorem of calculus, we obtain

Q9 :
Answer :

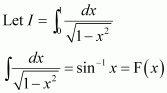
By second fundamental theorem of calculus, we obtain

Q10 :
Answer :

By second fundamental theorem of calculus, we obtain

Q11 :
Answer :

By second fundamental theorem of calculus, we obtain

Q12 :
Answer :

By second fundamental theorem of calculus, we obtain

Q13 :
Answer :

By second fundamental theorem of calculus, we obtain

Q14 :
Answer :

By second fundamental theorem of calculus, we obtain

Q15 :
Answer :

By second fundamental theorem of calculus, we obtain

Q16 :
Answer :
Let
Equating the coefficients of x and constant term, we obtain
A = 10 and B = – 25

Substituting the value of I₁ in (1), we obtain

Q17 :
Answer :

By second fundamental theorem of calculus, we obtain

Q18 :
Answer :

By second fundamental theorem of calculus, we obtain

Q19 :
Answer :

By second fundamental theorem of calculus, we obtain

Q20 :
Answer :

By second fundamental theorem of calculus, we obtain

Q21 : equals
A.
B.
C.
D.
Answer :

By second fundamental theorem of calculus, we obtain

Hence, the correct answer is D.

Q22 : equals
A.
B.
C.
D.
Answer :

By second fundamental theorem of calculus, we obtain

Hence, the correct answer is C.

Exercise 7.10 : Solutions of Questions on Page Number : 340

Q1 :
Answer :

When x = 0, t = 1 and when x = 1, t = 2

Q2 :
Answer :

When x = 0, t = 1 and when x = 1, t = 2

Q3 :
Answer :

Also, let

Q4 :
Answer :

Also, let

Q5 :
Answer :

Also, let x = tanθ ⇒ dx = sec2θ dθ
When x = 0, θ = 0 and when x = 1,

Takingθas first function and sec2θ as second function and integrating by parts, we obtain

Q6 :
Answer :

Also, let x = tanθ ⇒ dx = sec2θ dθ
When x = 0, θ = 0 and when x = 1,
Taking θ as first function and sec2θ as second function and integrating by parts, we obtain

Q7 :
Answer :

Let x + 2 = t² ⇒ dx = 2tdt
When x = 0, and when x = 2, t = 2

Q8 :
Answer :

Let x + 2 = t² ⇒ dx = 2tdt
When x = 0, and when x = 2, t = 2

Q9 :
Answer :

Let cos x = t ⇒ – sinx dx = dt
When x = 0, t = 1 and when

Q10 :
Answer :

Let cos x = t ⇒ – sinx dx = dt
When x = 0, t = 1 and when

Q11 :
Answer :

Let ⇒ dx = dt

Q12 :
Answer :

Let ⇒ dx = dt

Q13 :
Answer :

Let x + 1 = t ⇒ dx = dt
When x = – 1, t = 0 and when x = 1, t = 2

Q14 :
Answer :

Let x + 1 = t ⇒ dx = dt
When x = – 1, t = 0 and when x = 1, t = 2

Q15 :
Answer :

Let 2x = t ⇒ 2dx = dt
When x = 1, t = 2 and when x = 2, t = 4

Q16 :
Answer :
Let 2x = t ⇒ 2dx = dt
When x = 1, t = 2 and when x = 2, t = 4

Q17 : The value of the integral is
A. 6
B. 0
C. 3
D. 4
Answer :

Let cotθ = t ⇒ – cosec2θ dθ= dt

Hence, the correct answer is A.

Q18 : The value of the integral is
A. 6
B. 0
C. 3
D. 4
Answer :

Let cotθ = t ⇒ – cosec2θ dθ= dt

Hence, the correct answer is A.

Q19 : If
A. cos x + x sin x
B. x sinx
C. x cos x
D. sin x + x cos x
Answer :

Integrating by parts, we obtain

Hence, the correct answer is B.

Q20 : If
A. cos x + x sin x
B. x sinx
C. x cos x
D. sin x + x cos x
Answer :

Integrating by parts, we obtain

Hence, the correct answer is B.

Exercise 7.11 : Solutions of Questions on Page Number : 347

Q1 :
Answer :

Adding (1) and (2), we obtain

Q2 :
Answer :

Adding (1) and (2), we obtain

Q3 :
Answer :

Adding (1) and (2), we obtain

Q4 :
Answer :

Adding (1) and (2), we obtain

Q5 :Answer :

Adding (1) and (2), we obtain

Q6 :
Answer :
Adding (1) and (2), we obtain

Q7 :Answer :
Adding (1) and (2), we obtain

Q8 : Answer :

Q9 :
Answer :

Q10 :
Answer :

Adding (1) and (2), We obtain

Q11 : Answer :
As sin²(-x)=(sin(-x)) = (-sinx)²= sin2x, therefore, sin2x is an even function.
It is known that if f(x) is an even function,then

Q12 :
Answer :

Q13 :
Answer :

As sin⁷(-x)=(sin(-x))⁷=(-sinx)⁷=-sin⁷x,therefore,sin²x is an even function.
It is known that if f(x) is an even function,then

Q14 :
Answer :
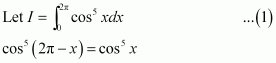It is known that,

Q15 :
Answer :

Adding (1) and (2), we obtain,

Q16 :
Answer :

Adding (1) and (2), we obtain,
sin(Π-x)=sinx

Adding (4) and (5), we obtain,

Q17 :
Answer :
It is known that,

Adding (1) and (2),we obtain,

Q18 :
Answer :
It can be seen that,(x-a) ≤ 0 when 0 ≤ x ≤1 and(x-1) ≥0 when 1 ≤ x ≤ 4.

Q19 : Show that if f and g defined asand
Answer :

Adding (1) and (2), we obtain

Q20 : The value of
A.0
B.2
C.Π
D.

Answer :
It is known that if f(x) is an even function,then
and f(x) is an odd function,then

Hence,the correct answer is C.

Q21 : The value of
A. 2
B. C. 0
D. -2

Answer :

Adding (1) and (2),we obtain,

Hence the correct answer is C.

Exercise Miscellaneous : Solutions of Questions on Page Number : 352

Q1 :
Answer :

Equating the coefficients of x², x, and constant term, we obtain
– A + B – C = 0
B + C = 0
A = 1
On solving these equations, we obtain
From equation (1), we obtain

Q2 :
Answer :

Q3 :
[Hint: Put]
Answer :

Q4 :
Answer :

Q5 :
Answer :

On dividing, we obtain

Q6 :
Answer :

Equating the coefficients of x², x, and constant term, we obtain
A + B = 0
B + C = 5
9A + C = 0
On solving these equations, we obtain
From equation (1), we obtain

Q7 :
Answer :
Let x – a = t ⇒ dx = dt

Q8 :
Answer :

Q9 :
Answer :
Let sin x = t ⇒ cos x dx = dt

Q10 :
Answer :

Q11 :
Answer :

Q12 :
Answer :
Let x⁴ =t ⇒ 4x³ dx = dt

Q13 :
Answer :
Let ex = t ⇒ e^x dx = dt

Q14 :
Answer :

Equating the coefficients of x³, x², x, and constant term, we obtain
A + C = 0
B + D = 0
4A + C = 0
4B + D = 1
On solving these equations, we obtain

From equation (1), we obtain

Q15 :

Answer :
= cos3 x × sin x
Let cos x = t ⇒ – sin x dx =dt

Q16 :
Answer :

Q17 :
Answer :

Q18 :
Answer :

Q19 :
Answer :

Q20 :
Answer :

Q21 :

Answer :

Q22 :
Answer :

Equating the coefficients of x², x,and constant term, we obtain
A + C = 1
3A + B + 2C = 1
2A + 2B + C = 1
On solving these equations, we obtain
A = – 2, B = 1, and C = 3
From equation (1), we obtain